宇宙の神秘の法則に迫る・・・惑星軌道の不思議
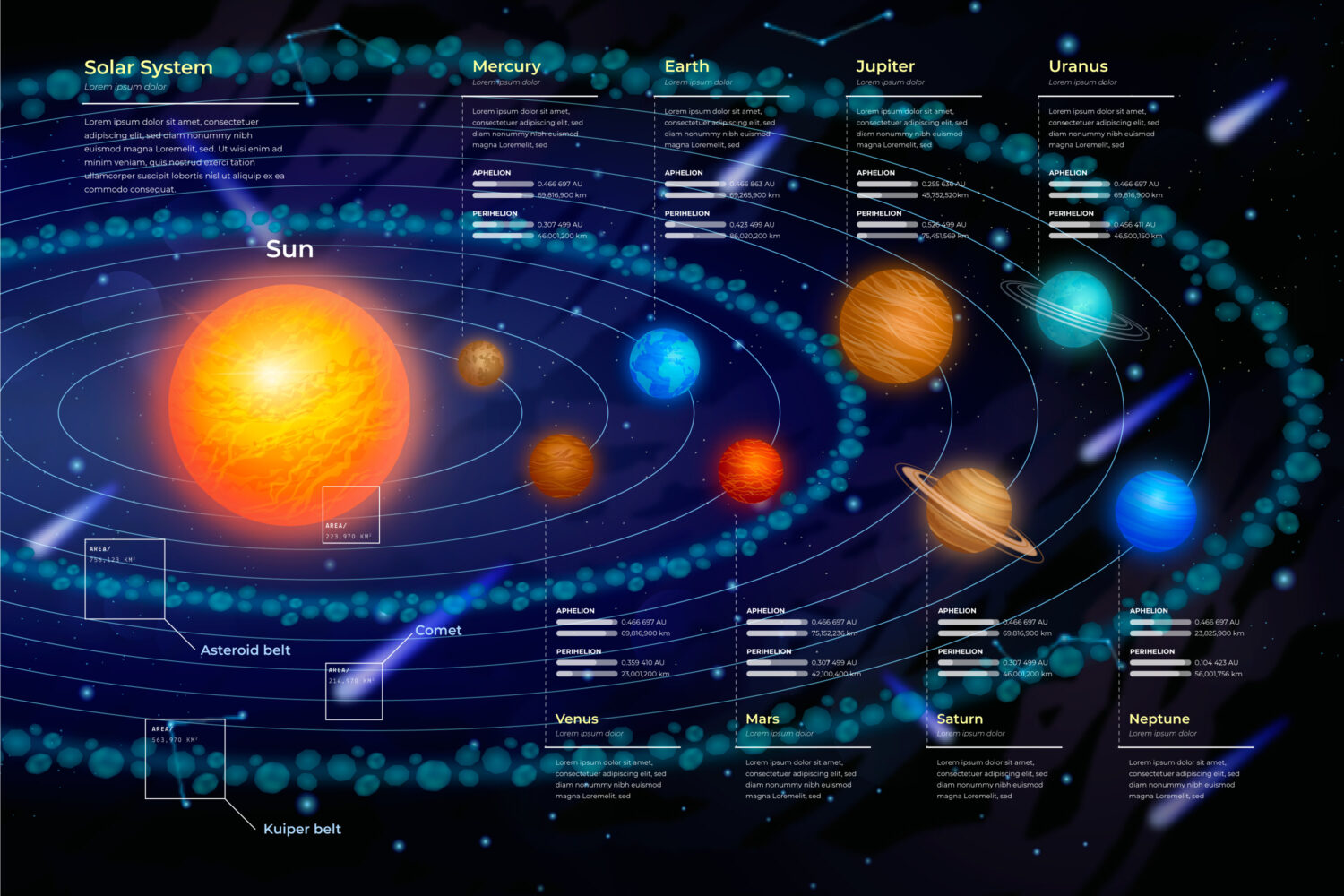
それは、私達人類が誕生するよりもずっと前から決まっていた法則です。
一番目の神秘の法則
天体の法則として、不思議なのは惑星や衛星が楕円軌道を描いていることです。
地球も月も火星も木星も楕円軌道を描いています。
そして、彗星(ほうき星)も、その軌道は楕円なのです。
楕円軌道の中の太陽
楕円とは、中心となる点がふたつある長めの丸い図形です。
このふたつの中心を「焦点」と呼びます。
惑星は楕円軌道ですがふたつの焦点のうちのどちらかに太陽が位置しています。
これも不思議なことです。
もうひとつの焦点には何もいません。
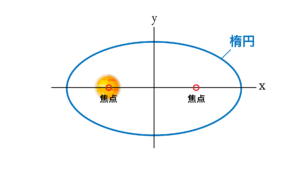
ケプラーの第一法則 楕円軌道の法則
焦点の距離は軌道の形にかかわる
焦点がとてつもなく離れていると、とっても長細い楕円軌道になります。
彗星がそうですね。
彗星の軌道は、太陽の直ぐ側を通ったかと思うと、海王星より外側に行くのもあります。
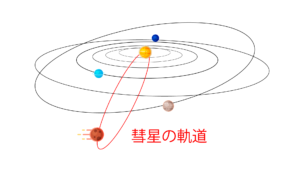
彗星の軌道
逆に焦点がかなり近いと楕円が円のようになります。
もし、2つの焦点が近づき過ぎて重なってしまったら、真円です。
ですから、円も楕円のひとつの姿です。
条件が整った特別な楕円と言ってよいでしょう。
この法則はあまりにも都合がいいので、つい疑ってしまいそうですが、本当なのです。
宇宙の神秘と呼ぶ以外ありません。
二番目の神秘の法則
宇宙の神秘の法則は他にもあります。
扇型の面積も神秘
楕円軌道を描く惑星と、太陽を直線で結んだとします。
この直線は時間が経つと少しずつ動いていきますが、この直線が描いた図形は扇形みたいになりますよね。
例えば地球は1年をかけて太陽の周りを回るので、1ヶ月でおよそ30度動きます。
この扇形は、地球の動いた時間が同じだと、面積も同じになるのです。
ですから、1月に描いた扇形と、8月に描いた扇形は同じ面積です。
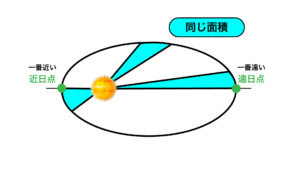
ケプラーの第二法則 面積速度一定の法則
これも不思議な現象です。
楕円だから距離が変わる
惑星は楕円軌道なので太陽に近い時期と遠い時期があります。
太陽と惑星の距離が最も近い時は「近日点」と呼ばれています。
逆の遠いときは「遠日点」ですね。
それなのに一定時間で描く扇型が同じだなんて、とても良くできていますよね。
宇宙の神秘ですよね。
彗星の扇形は極端
地球は楕円軌道と言っても、かなり真円に近いので扇型の形は極端には変わりません。
30日で描く扇型は4月も6月も9月も11月もほとんど同じです。
しかし彗星はどうでしょう。
太陽にものすごく接近する時期は、とてつもない速さになります。
ですが、太陽から遠く離れたところでは、極端に遅くなります。
それでも一定時間に描く扇形の面積は同じなのです。
同じ時間であっても太陽近くでの扇形はかなり開いています。
しかし太陽から離れているとほとんど開かれていない扇型になってしまいます。
三番目の神秘の法則
惑星の公転周期は遠くなればなるほど長くなります。
これはなんとなく分かりますよね。
水星や金星は早く回って、天王星や海王星は長い時間かかって太陽の周りを回ります。
公転周期と楕円の直径の関係
この公転周期は軌道である楕円から計算式で求まるというのです。
「公転周期の2乗」と「楕円の長い方の直径の3乗」の比率が、どの惑星も一定なのです。
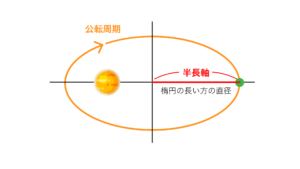
ケプラーの第三法則 調和の法則
これも不思議です。
楕円軌道の形がわかっていれば、どれぐらいの時間をかけて惑星が太陽を一周するのか、計算で分かります。
宇宙の神秘と呼ぶにふさわしいお話です。
偉大な天文学者
今回ご紹介した宇宙の神秘を一つにまとめた人がいます。
それが、16世紀ドイツの天文学者ヨハネス・ケプラーです。

ヨハネス・ケプラー
紹介した順番に名前がついています。
- ケプラーの第一法則 楕円軌道の法則
- ケプラーの第二法則 面積速度一定の法則
- ケプラーの第三法則 調和の法則
最初のふたつはすぐにピンときますが、さすがに3つ目のネーミングはわかりにくいですよね。
それはともかく、宇宙の神秘を法則に迫るのが天文学者たちです。
それまでわからなかった宇宙のことが次第に明らかになっています。
見えない法則を人々は神秘と呼びます。
そして、その法則を操るものを畏れ(おそれ)ます。
さらに、その法則の謎に迫りたいと考えます。
それは人類の夢なのかもしれません。
本サイトに掲載されているすべての内容の著作権は運営者に帰属しております。
本サイトの掲載内容(画像、文章等)の一部及び全てについて、無断で複製、転載、転用、改変等の二次利用を固く禁じます。 上記著作権の無断複製、転載、転用、改変等が判明した場合は、法的措置をとる場合がございます。

